# 绘制散点图或气泡图
# 使用 scatter() 绘制散点图或气泡图
# 使用pyplot 的 scatter() 函数可以快速绘制散点图或气泡图,scatter() 函数的语法格式如下所示 :
scatter (x, y, s=None, c=Ncne, marker=None, cmap=None, norm=None,
vmin=None, vmax=None, alpha=None, linewidths=None, verts=None,
edgecolors=None, *, plotnonfinite=False, data=None, **kwargs)
# 该函数常用参数的含义如下。
# · x, y :表示数据点的位置。
· s :表示数据点的大小。
· C :表示数据点的颜色。
· marker :表示数据点的样式,默认为圆形。
· cmap :表示数据点的颜色映射表,仅当参数 c 为浮点数组时才使用。
· norm :表示数据亮度,可以取值为 0 ~ 1。
· vmin, vmax :表示亮度的最小值和最大值。若传入了 norm 参数,则忽略 vmin 和vmax 参数。
· alpha :表示透明度,可以取值为 0 ~ 1。
· linewidths :表示数据点边缘的宽度。
· edgecolors :表示数据点边缘的颜色。
# 使用 scatter() 函数绘制一个散点图,代码如下。
In [19]:
num = 50
x = np.random.rand(num)
y = np.random.rand(num)
plt.scatter(x, y)
# 使用scatter() 函数绘制一个气泡图,代码如下。
In [20]:
num = 50
x = np.random.rand(num)
y = np.random.rand(num)
area = (30 * np.random.rand(num))**2
plt.scatter(x, y, s=area)
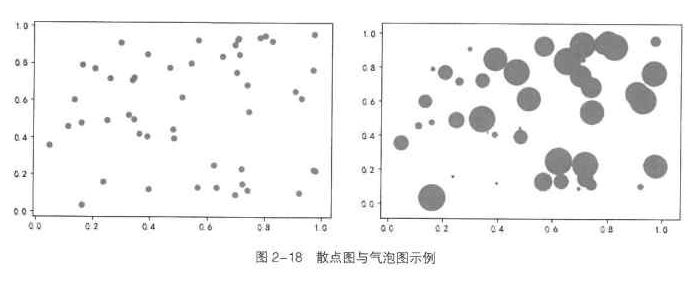
# 两个示例运行的效果如图 2-18 所示。
# 实例7:汽车速度与制动距离的关系
# 汽车的制动距离主要取决于车速。若车速增加 1 倍,则汽车的制动距离将增大至近 4 倍。某汽车生产公司对一批丰田汽车进行抽样测试,并分别记录了不同的车速对应的制动距离,具体如表 2-6 所示。
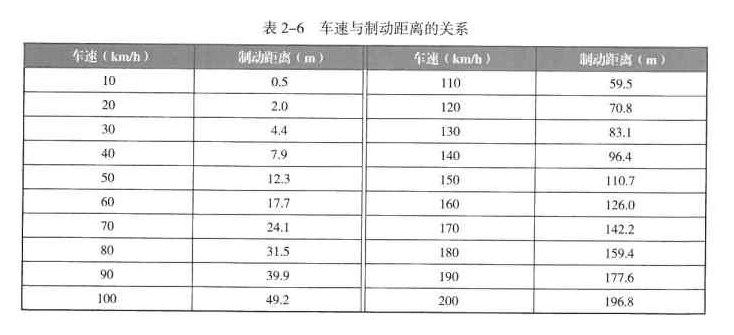
# 根据表 2-6 的数据,将 “车速(km/h)” 一列的数据作为 x 轴的数据,将 “制动距离(m)” 一列的数据作为 y 轴的数据,使用 scatter() 函数绘制汽车速度与制动距离关系的散点图,具体代码如下。
In [21]:
# 07_vehicle_speed__and__braking_distance
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.reParams ['axes.unicode__minus'] = False
# 准备 x 轴和 y 轴的数据
x_speed = np.arange(10, 210, 10)
y__distance = np.array([0.5, 2.0, 4.4, 7.9, 12.3,
17.7, 24.1, 31.5, 39.9, 49.2,
59.5, 70.8, 83.1, 96.4, 110.7,
126.0, 142.2, 159.4, 177.6, 196.8])
# 绘制散点图
plt.scatter(x_speed, y_distance, s=50, alpha=0.9)
plt.show ()
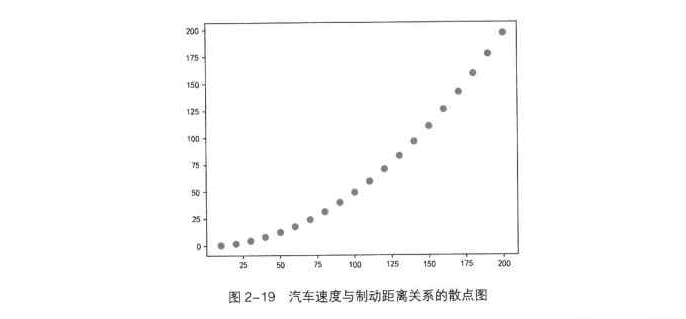
# 运行程序,效果如图 2-19 所示。