# 填充区域
# 填充多边形或曲线之间的区域
# matplotlib 中提供了多个函数用于填充多边形或区域,分别为 fill() 、 fill_between() 和 fill_betweenx() 。其中,fill() 函数用于填充多边形 ;fill_between() fill_betweenx() 函数分别用于填充两条水平曲线或垂直曲线之间的区域。下面介绍 fill() 、fill_between() 和 fill_betweenx() 函数的用法。
# 使用 fill() 函数填充多边形
# fill() 函数的语法格式如下所示 :
fill(*args, data=None, facecolor, edgecolor, linewidth, **kwargs)
# 该函数常用参数的含义如下。
# · *args :表示 x 轴坐标、y 轴坐标或颜色的序列。
· facecolor :表示填充的背景颜色。
· edgecolor :表示边框的颜色。
· linewidth :表示边框的宽度。
# 填充多边形的示例代码如下 :
plt.fill(x, y) # 使用默认颜色填充多边形
plt.fill(x, y, "b") # 使用指定颜色填充多边形
plt.fill(x, y, x2, y2) # 使用默认颜色填充两个多边形
plt.fill(x, y, "b", x2, y2, "r") # 使用指定颜色填充两个多边形
# 使用 fill_between() 函数填充两条水平曲线之间的区域
# fill_between() 函数的语法格式如下所示 :
fill_between(x, y1, y2=0, where=None, interpolate=False, step=None,
data=None, **kwargs)
# 该函数常用参数的含义如下。
# · x :表示 x 轴坐标的序列。
· y1 :表示第一条曲线的 y 轴坐标。
· y2 :表示第二条曲线的y轴坐标。
· where :布尔值,表示要填充区域的条件。y1 > y2 说明第一条曲线位于第二条曲线上方时填充 ;y1 < y2 说明第二条曲线位于第一条曲线上方时填充。
# 使用 fill_betweenx() 函数填充两条垂直曲线之间的区域
# fill_betweenx() 函数的语法格式如下 :
fill_betweenx(y, x1, x2=0, where=None, step=None, interpolate=False,
data=None, **kwargs)
# 该函数常用参数的含义如下 :
# · y :表示 y 轴坐标的序列。
· x1 :表示第一条曲线的 x 轴坐标。
· x2 :表示第二条曲线的 x 轴坐标。
· where :布尔值,表示要填充区域的条件。x1 > x2 说明第一条曲线位于第二条曲线右方时填充 ;x1 < x2说明第二条曲线位于第一条曲线右方时填充。
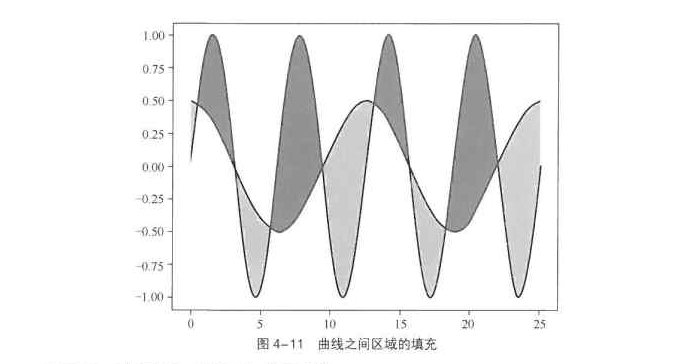
# 例如,将第一条曲线位于第二条曲线上方的区域填充为蓝色,将第一条曲线位于第二条曲线下方的区域填充为橙色,代码如下 :
plt.fill_between(x, cos_y, sin_y, cos_y < sin_y, color='dodgerblue',
alpha=0.5)
plt.fill_between(x, cos_y, sin_y, cos_y > sin_y, colors='orangered',
alpha=0.5)
# 以上示例的填充效果如图 4-11 所示。
# 实例5:彩色的“雪花”
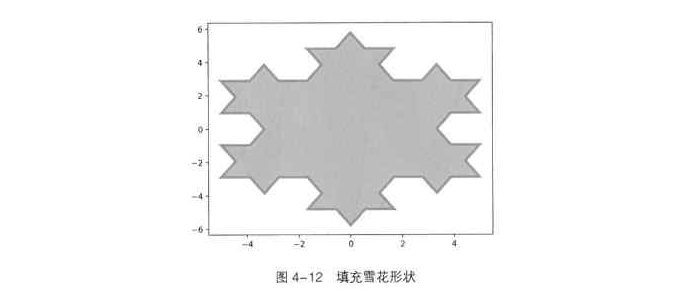
# 雪花一般呈六角形,且通体为白色。下面使用 matplotlib 绘制一个由六角形组成的雪花形状的多边形,并将多边形填充为浅橙色,具体代码如下。
In [9]:
# 05_colorful_snowflakes
import numpy as np
import matplotlib.pyplot as plt
def koch_snowflake(order, scale=10):
def_koch_snowflake_complex(order):
if order == 0:
# 初始三角形
angles = np.array([0, 120, 240]) + 90
return scale / np.sqrt(3) * np.exp(np.deg2rad(angles) * 1j)
else:
ZR = 0.5 - 0.5j * np/sqrt(3) / 3
p1 = _koch_snowflake_complex(order - 1) # 起点
p2 = np.roll(p1, shift=-1) # 终点
dp = p2 - p1 # 连接向量
new_points = np.empty(len(p1) * 4, dtype=np.complex128)
new_points[::4] = p1
new_points[1::4] = p1 + dp / 3
new_points[2::4] = p1 + dp * ZR
new_points[3::4] = p1 + dp / 3 * 2
return new_points
points = _koch_snowflake_conplex(order)
x, y = points.real, points.imag
return x, y
x, y = koch_snowflake(order=2)
fig = plt.figure()
ax = fig.add_subplot (111)
ax.fill(x, y, facecolor='lightsalmon', edgecolor='orangered' , linewidth=3)
plt.show ()
# 运行程序,效果如图 4-12 所示。